Jak uczyć się matematyki? Opanuj ją raz na zawsze!

Wielu z nas kojarzy matematykę z frustracją, niezrozumiałymi wzorami i niekończącymi się zadaniami. Jeśli czujesz, że matematyka to dla Ciebie czarna magia, ten artykuł jest właśnie dla Ciebie. Pokażę Ci, że skuteczna nauka matematyki jest w zasięgu ręki, niezależnie od Twoich wcześniejszych doświadczeń czy przekonań o „braku talentu”. Razem odkryjemy sprawdzone metody, które pomogą Ci zrozumieć, polubić i w końcu opanować ten fascynujący przedmiot.

Zrozum, dlaczego matematyka bywa trudna i zmień swoje nastawienie

Zanim zagłębimy się w konkretne techniki, musimy zmierzyć się z czymś, co często blokuje nas już na starcie: naszym nastawieniem do matematyki. Wielu uczniów, a nawet dorosłych, postrzega ten przedmiot jako coś nieosiągalnego, zarezerwowanego tylko dla "wybrańców". Ja sam widziałem, jak to błędne przekonanie potrafi zniszczyć motywację do nauki.

Czy to „matematykofobia”? Jak rozpoznać i przełamać lęk przed liczbami

Lęk przed matematyką, często nazywany matematykofobią, to realne zjawisko, które dotyka wielu osób. Objawia się on niepokojem, stresem, a nawet paniką na samą myśl o rozwiązywaniu zadań czy egzaminie z matematyki. Z moich obserwacji i danych wynika, że to jeden z głównych problemów, z którymi zmagają się polscy uczniowie. Często korzenie tego lęku tkwią w negatywnych doświadczeniach z przeszłości, presji otoczenia lub braku zrozumienia podstawowych pojęć.

Jak rozpoznać, czy dotyka Cię matematykofobia? Zastanów się, czy czujesz fizyczne objawy stresu przed lekcjami matematyki, czy unikasz zadań z nią związanych, czy masz poczucie, że "nie dasz rady", zanim jeszcze spróbujesz. Pierwszym krokiem do przełamania tego lęku jest uświadomienie sobie jego istnienia i zaakceptowanie go. Następnie musimy zmienić nastawienie zamiast postrzegać matematykę jako wroga, spróbujmy spojrzeć na nią jak na wyzwanie, które można pokonać. Budowanie pewności siebie zaczyna się od małych sukcesów. Nie bój się prosić o pomoc i pamiętaj, że każdy ma prawo do błędów.

Pułapka „braku talentu”: dlaczego systematyczność jest ważniejsza niż wrodzone zdolności

Jednym z najbardziej szkodliwych mitów, jakie słyszę, jest ten o "braku talentu" do matematyki. Wiele osób, gdy napotka trudności, automatycznie przypisuje je wrodzonym predyspozycjom, mówiąc: "Ja po prostu nie jestem do tego stworzony". Nic bardziej mylnego! Dane jasno pokazują, że kluczem do sukcesu w matematyce jest systematyczność i regularna praca, a nie jakiś mityczny "talent". Oczywiście, niektórzy mają większą łatwość w przyswajaniu pewnych koncepcji, ale nawet oni bez konsekwentnej pracy nie osiągną mistrzostwa. Konsekwentna praca, nawet w małych dawkach, buduje solidne fundamenty i pozwala na stopniowe zrozumienie coraz bardziej złożonych zagadnień. To tak jak z budowaniem mięśni nie zyskasz ich po jednym intensywnym treningu, ale po regularnych ćwiczeniach przez dłuższy czas. Matematyka to maraton, nie sprint.

Błędy, które hamują Twój postęp: od braków w podstawach po złe nawyki w nauce

Z mojego doświadczenia wynika, że wiele trudności w nauce matematyki wynika z powtarzających się błędów i złych nawyków. Oto najczęstsze z nich:

• Braki w podstawach: To chyba najpoważniejszy problem. Matematyka to przedmiot hierarchiczny. Jeśli nie rozumiesz ułamków, trudno będzie Ci opanować równania. Jeśli brakuje Ci podstaw z poprzednich lat edukacji, każda nowa lekcja będzie budowana na chwiejnym gruncie.
• Nacisk na schematyczne rozwiązywanie: Zamiast zrozumieć, dlaczego coś działa, uczniowie często uczą się na pamięć schematów rozwiązywania zadań. Wystarczy drobna zmiana w treści zadania, a już pojawia się problem, bo schemat nie pasuje.
• Postrzeganie matematyki jako zbioru niezwiązanych wzorów: Wielu uczniów widzi matematykę jako chaotyczny zbiór wzorów i definicji, które trzeba zapamiętać. Brakuje im umiejętności łączenia różnych działów i dostrzegania logicznych powiązań.
• Brak systematyczności: Uczenie się "na ostatnią chwilę" przed sprawdzianem to przepis na katastrofę. Wiedza przyswojona w ten sposób szybko ulatuje.
• Unikanie trudnych zadań: Koncentrowanie się tylko na tym, co łatwe, nie pozwala na rozwój i pokonywanie własnych barier.
• Nieanalizowanie błędów: Popełnianie błędów jest naturalne, ale kluczowe jest wyciąganie z nich wniosków. Jeśli nie wiesz, dlaczego coś poszło źle, będziesz powtarzać te same pomyłki.

Fundamenty skutecznej nauki: Zbuduj solidną bazę wiedzy matematycznej

Skuteczna nauka matematyki to jak budowanie domu potrzebujesz solidnych fundamentów. Bez nich cała konstrukcja będzie niestabilna. W tej sekcji skupimy się na tym, jak zbudować taką bazę, aby każda kolejna cegiełka wiedzy układała się w spójną całość.

Krok 1: Zdiagnozuj swoje braki od czego naprawdę musisz zacząć?

Zanim zaczniesz intensywną naukę, musisz wiedzieć, gdzie stoisz. To absolutnie kluczowe. Jak wspomniałem wcześniej, braki w podstawach to najczęstsza przyczyna problemów. Nie ma sensu uczyć się trygonometrii, jeśli nie rozumiesz geometrii podstawowej. Moja rada to zacząć od diagnozy. Możesz to zrobić, rozwiązując testy diagnostyczne z poprzednich lat (często dostępne online lub w podręcznikach), przeglądając materiał z poprzednich klas i sprawdzając, które zagadnienia sprawiają Ci trudność. Nie bój się wrócić do materiału z podstawówki czy gimnazjum, jeśli to konieczne. To nie wstyd, to mądra strategia. Lepiej poświęcić czas na uzupełnienie luk teraz, niż ciągle potykać się o te same problemy w przyszłości.

Krok 2: Zrozumieć, a nie zakuć dlaczego zadawanie pytań „dlaczego?” jest kluczowe

Pamięciowe opanowanie wzorów i definicji to droga donikąd. Matematyka to nie zbiór magicznych zaklęć, ale logiczny system. Dlatego tak mocno podkreślam: zrozumienie jest ważniejsze niż zapamiętywanie. Zawsze zadawaj sobie pytanie: "Dlaczego to działa w ten sposób?". Dlaczego ten wzór wygląda tak, a nie inaczej? Skąd się wziął? Jakie są jego ograniczenia? Aktywne poszukiwanie odpowiedzi na te pytania zmusza Twój mózg do głębszego przetwarzania informacji, łączenia ich z już posiadaną wiedzą i budowania spójnej siatki pojęć. Kiedy zrozumiesz logikę stojącą za danym zagadnieniem, wzory same "wskoczą" na swoje miejsce, a Ty będziesz w stanie zastosować je w różnych kontekstach, nawet tych niestandardowych.

Krok 3: Potęga systematyczności stwórz plan nauki, który naprawdę działa (i którego będziesz się trzymać)

Systematyczność to Twój najlepszy przyjaciel w nauce matematyki. Krótkie, regularne sesje nauki (np. 30-45 minut dziennie) są o wiele efektywniejsze niż kilkugodzinne zrywy raz w tygodniu. Dzieje się tak, ponieważ mózg lepiej przyswaja informacje w mniejszych dawkach, a regularne powtórki utrwalają wiedzę. Oto jak stworzyć realistyczny i skuteczny plan nauki:

1. Oceń swój czas: Zastanów się, ile realnie możesz poświęcić na matematykę każdego dnia. Bądź szczery ze sobą. Lepiej zaplanować 30 minut i je zrealizować, niż zaplanować 2 godziny i ciągle odkładać naukę.
2. Wyznacz konkretne pory: Wprowadź naukę matematyki do swojego codziennego harmonogramu jak stały element, np. "codziennie po obiedzie" lub "przed wieczornym serialem".
3. Podziel materiał na małe części: Nie próbuj opanować całego działu naraz. Skup się na jednym, konkretnym zagadnieniu na sesję.
4. Zaplanuj powtórki: W swoim planie uwzględnij czas na powtórki materiału z poprzednich dni i tygodni. To klucz do trwałego zapamiętywania.
5. Bądź elastyczny, ale konsekwentny: Życie bywa nieprzewidywalne. Jeśli jeden dzień wypadnie z planu, nie rezygnuj. Po prostu wróć do niego następnego dnia. Ważna jest konsekwencja w długim terminie.
6. Nagradzaj się: Po każdej zrealizowanej sesji nauki, pozwól sobie na małą nagrodę. To wzmacnia pozytywne skojarzenia z nauką.

Krok 4: Notatki, które pomagają jak wizualizować pojęcia i tworzyć mapy myśli

Dobre notatki to nie tylko spis treści, ale narzędzie, które aktywnie wspiera proces uczenia się. W matematyce szczególnie ważne jest, aby notatki były czytelne, uporządkowane i wizualne. Pamiętaj, że wizualizacja problemów matematycznych znacząco ułatwia ich zrozumienie. Oto kilka wskazówek:

• Używaj kolorów: Różne kolory mogą pomóc w wyróżnieniu ważnych wzorów, definicji, przykładów czy błędów.
• Rysuj schematy i diagramy: Zamiast opisywać słowami, jak wygląda wykres funkcji, po prostu go narysuj. Twórz schematy blokowe dla procesów rozwiązywania zadań.
• Twórz mapy myśli: Mapy myśli to doskonały sposób na wizualne przedstawienie powiązań między różnymi pojęciami. Centralny temat (np. "Funkcja kwadratowa") otocz gałęziami z kluczowymi informacjami (wzory, wykresy, zastosowania, przykłady).
• Zostawiaj dużo miejsca: Nie upychaj wszystkiego na jednej stronie. Zostaw wolne miejsce na dodatkowe notatki, komentarze czy rysunki, które przyjdą Ci do głowy później.
• Pisz własnymi słowami: Przepisywanie definicji z książki to pasywna nauka. Spróbuj przetłumaczyć je na swój własny, zrozumiały język.

Sprawdzone techniki, które odmienią Twoją naukę matematyki

Gdy już zbudujesz solidne fundamenty i zmienisz swoje nastawienie, czas na konkretne narzędzia, które przyspieszą i pogłębią Twoje zrozumienie matematyki. Te techniki są wykorzystywane przez najlepszych studentów i naukowców, a ich skuteczność jest potwierdzona.

Technika Feynmana w praktyce: Naucz się tłumaczyć matematykę na „ludzki” język

Technika Feynmana to potężne narzędzie, które pozwala nie tylko sprawdzić swoje zrozumienie, ale także je pogłębić. Polega ona na tym, że próbujesz wytłumaczyć dane zagadnienie matematyczne komuś, kto nie ma o nim pojęcia, używając prostego, zrozumiałego języka. Richard Feynman, laureat Nagrody Nobla, uważał, że jeśli nie potrafisz czegoś prosto wytłumaczyć, to sam tego nie rozumiesz. Oto jak ją zastosować:

1. Wybierz zagadnienie: Wybierz konkretny temat, wzór lub definicję, którą chcesz opanować (np. "pochodna funkcji", "równanie kwadratowe").
2. Wytłumacz to: Spróbuj wytłumaczyć to zagadnienie, jakbyś mówił do dziecka lub osoby, która nigdy nie miała z tym styczności. Używaj prostych słów, unikaj żargonu. Możesz mówić na głos, pisać na kartce lub tablicy.
3. Zidentyfikuj luki: Podczas tłumaczenia z pewnością natkniesz się na miejsca, w których Twoje wyjaśnienie jest niejasne, brakuje Ci słów lub po prostu "wiesz, że wiesz, ale nie potrafisz tego wyjaśnić". To są Twoje luki w zrozumieniu.
4. Wróć do źródła: Gdy zidentyfikujesz lukę, wróć do podręcznika, notatek lub innych źródeł i uzupełnij swoją wiedzę w tym konkretnym punkcie.
5. Uprość i powtórz: Po uzupełnieniu luki, spróbuj ponownie wytłumaczyć całe zagadnienie, tym razem starając się jeszcze bardziej uprościć język i strukturę. Powtarzaj ten proces, aż będziesz w stanie wyjaśnić temat jasno i zwięźle.

Active Recall i Spaced Repetition: Jak zapamiętywać wzory i definicje na stałe

Pamięć to nie magazyn, do którego wrzucasz informacje. To mięsień, który trzeba trenować. Dwie techniki, które rewolucjonizują proces zapamiętywania, to Aktywne Przypominanie (Active Recall) i Powtarzanie w Odstępach (Spaced Repetition).

Aktywne przypominanie polega na celowym odtwarzaniu informacji z pamięci, zamiast biernego ich odczytywania. Zamiast czytać definicję z podręcznika, spróbuj ją najpierw samodzielnie przypomnieć. To aktywnie wzmacnia połączenia neuronowe i utrwala wiedzę. Spaced Repetition to z kolei system powtórek, który zakłada, że informacje powinny być powtarzane w coraz dłuższych odstępach czasu. Im lepiej znasz dany materiał, tym rzadziej musisz go powtarzać. System ten optymalizuje proces zapamiętywania, koncentrując się na tych informacjach, które są dla Ciebie najtrudniejsze.

Jak stosować te techniki w praktyce:

• Fiszki: Twórz fiszki z definicjami, wzorami, twierdzeniami. Na jednej stronie pytanie (np. "Wzór na pole trójkąta"), na drugiej odpowiedź. Przeglądaj je regularnie, odkładając te, które znasz, i częściej powtarzając te, które sprawiają Ci trudność.
• Samodzielne testowanie: Po każdej sesji nauki zamknij książkę i spróbuj przypomnieć sobie kluczowe pojęcia, wzory i kroki rozwiązywania zadań. Możesz to zrobić, pisząc je na kartce lub mówiąc na głos.
• Pytania kontrolne: Po każdym akapicie lub rozdziale zadawaj sobie pytania, które zmuszą Cię do przypomnienia sobie treści, zamiast ją tylko biernie czytać.
• Aplikacje do Spaced Repetition: Skorzystaj z aplikacji takich jak Anki, które automatycznie planują powtórki fiszek, bazując na algorytmie Spaced Repetition.

Potęga wizualizacji: Rysuj, kreśl i twórz schematy, aby zrozumieć abstrakcyjne problemy

Matematyka często operuje na abstrakcyjnych pojęciach, co może być trudne dla naszego mózgu, który uwielbia obrazy. Dlatego wizualizacja jest tak potężnym narzędziem. Rysowanie, kreślenie i tworzenie schematów pomaga przełożyć abstrakcję na coś konkretnego i namacalnego.

Na przykład, ucząc się o funkcjach, zawsze rysuj ich wykresy. Zobacz, jak zmienia się parabola, gdy zmieniasz współczynniki. Rozwiązując zadania z geometrii, zawsze zaczynaj od dokładnego rysunku. W algebrze, gdy masz do czynienia z układami równań, wyobraź sobie, że każda zmienna to inny element, a równania to zasady, które je łączą. Możesz nawet rysować małe ikonki, które symbolizują zmienne. Przy problemach z prawdopodobieństwem, rysuj drzewka decyzyjne, aby zobaczyć wszystkie możliwe scenariusze. Wizualizacja pomaga również w zrozumieniu problemów tekstowych spróbuj narysować sytuację opisaną w zadaniu, zanim przejdziesz do obliczeń.

Od teorii do praktyki: Dlaczego samodzielne rozwiązywanie zadań jest absolutnie kluczowe

Możesz przeczytać setki książek, obejrzeć dziesiątki filmów i zrozumieć każdą definicję, ale jeśli nie zaczniesz samodzielnie rozwiązywać zadań, Twoja wiedza będzie pasywna i niepełna. Samodzielne rozwiązywanie zadań to absolutnie kluczowy element opanowania matematyki. To właśnie wtedy teoria zderza się z praktyką, a Ty musisz aktywnie zastosować to, czego się nauczyłeś.

Pasywne przyswajanie wiedzy daje złudne poczucie zrozumienia. Dopiero gdy zmierzysz się z problemem i samodzielnie znajdziesz drogę do rozwiązania, Twoja wiedza staje się trwała i użyteczna. Rozwiązywanie zadań pozwala Ci testować różne strategie, popełniać błędy (i uczyć się na nich!), a także budować pewność siebie. Nie bój się popełniać błędów to naturalna część procesu nauki. Ważne jest, aby po każdym zadaniu, niezależnie od wyniku, przeanalizować swoje podejście i wnioski.

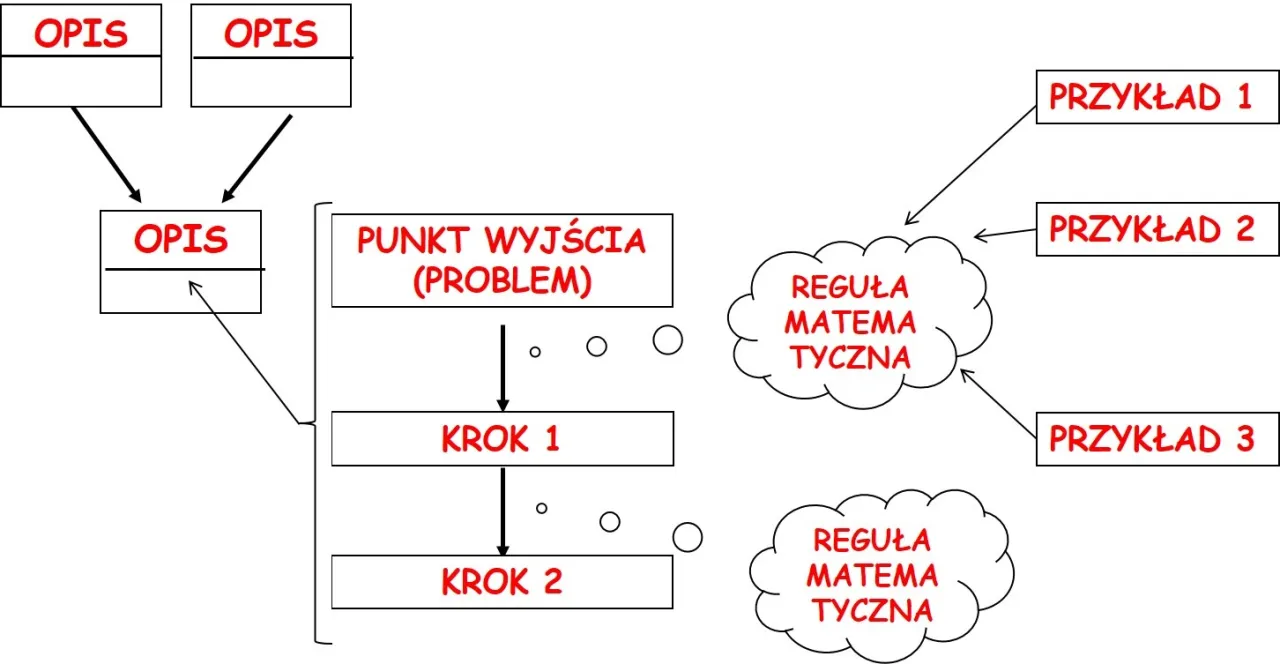
Pracuj z zadaniami efektywnie, aby uczyć się szybciej

Rozwiązywanie zadań to serce nauki matematyki, ale samo ich rozwiązywanie nie wystarczy. Musimy robić to efektywnie. Pokażę Ci, jak podejść do zadań w sposób, który maksymalizuje Twoje postępy i minimalizuje frustrację.

Anatomia zadania matematycznego: Jak czytać polecenia ze zrozumieniem i analizować dane

Zanim zaczniesz cokolwiek liczyć, musisz dokładnie zrozumieć, czego zadanie od Ciebie wymaga. Wiele błędów wynika z niedokładnego przeczytania polecenia. Oto kroki do efektywnej analizy zadania:

1. Przeczytaj polecenie dwukrotnie: Za pierwszym razem dla ogólnego zrozumienia, za drugim dla wychwycenia szczegółów.
2. Podkreśl kluczowe informacje: Wyróżnij dane liczbowe, jednostki, warunki brzegowe i słowa kluczowe, które wskazują na rodzaj operacji (np. "oblicz", "udowodnij", "znajdź", "ile razy więcej").
3. Zidentyfikuj cel zadania: Co dokładnie masz znaleźć lub udowodnić? Upewnij się, że wiesz, do czego dążysz.
4. Zapisz dane i szukane: Stwórz listę wszystkich podanych informacji i tego, co musisz obliczyć. To pomaga uporządkować myśli.
5. Narysuj schemat/rysunek (jeśli to możliwe): Wizualizacja problemu często ujawnia ukryte zależności i ułatwia zrozumienie.
6. Zastanów się nad kontekstem: Czy to zadanie z algebry, geometrii, czy analizy? Jakie wzory i twierdzenia z tego działu mogą być przydatne?

Strategie rozwiązywania problemów: Co robić, gdy utkniesz w martwym punkcie?

Każdy z nas utyka czasem w martwym punkcie. To naturalne. Ważne jest, aby mieć strategie, które pomogą Ci się z niego wydostać, zamiast poddawać się frustracji. Oto co ja robię w takich sytuacjach:

• Uprość problem: Jeśli zadanie jest zbyt złożone, spróbuj rozwiązać jego prostszą wersję. Zmień liczby na mniejsze, zredukuj liczbę zmiennych. Gdy zrozumiesz prostszy przypadek, łatwiej będzie Ci wrócić do oryginału.
• Rysuj, kreśl, wizualizuj: Czasem wystarczy narysować problem w inny sposób, aby zobaczyć nowe perspektywy.
• Szukaj podobnych przykładów: Przypomnij sobie, czy rozwiązywałeś kiedyś podobne zadanie. Jakie techniki tam zastosowałeś?
• Zrób przerwę: Czasem najlepszym rozwiązaniem jest chwilowe oderwanie się od zadania. Idź na spacer, napij się wody, zrób coś zupełnie innego. Twój mózg będzie pracował nad problemem w tle, a Ty wrócisz z nową energią i świeżym spojrzeniem.
• Pracuj wstecz: Jeśli znasz wynik (np. w zadaniach z dowodzeniem), spróbuj pracować od końca, krok po kroku, aż dojdziesz do danych.
• Porozmawiaj z kimś: Nawet samo opowiedzenie problemu komuś innemu (nawet jeśli ta osoba nie rozumie matematyki) może pomóc Ci uporządkować myśli i znaleźć rozwiązanie.

Twoje błędy to skarb: Jak analizować pomyłki, by nigdy więcej ich nie powtarzać

Błędy to nie porażki, ale najcenniejsze źródło nauki. Zamiast się ich bać, powinieneś je celebrować! Każdy błąd to informacja zwrotna, która wskazuje, gdzie masz luki w zrozumieniu lub gdzie Twoje podejście jest błędne. Z moich obserwacji wynika, że uczniowie, którzy systematycznie pracują na błędach, robią największe postępy.

Oto proces analizowania pomyłek:

1. Nie ignoruj błędu: Nigdy nie przechodź dalej, dopóki nie zrozumiesz, dlaczego popełniłeś błąd.
2. Zidentyfikuj typ błędu: Czy to błąd rachunkowy? Błąd w zastosowaniu wzoru? Błąd w zrozumieniu polecenia? Błąd logiczny?
3. Znajdź przyczynę: Dlaczego ten błąd się pojawił? Czy to brak wiedzy? Niedokładność? Pośpiech?
4. Popraw i zapisz: Popraw błąd, a następnie zapisz go w specjalnym zeszycie lub sekcji notatek, wraz z poprawnym rozwiązaniem i wyjaśnieniem, dlaczego poprzednie podejście było błędne.
5. Powtórz podobne zadania: Po zrozumieniu błędu, rozwiąż kilka podobnych zadań, aby upewnić się, że nowa wiedza została utrwalona.

Rola zadań z życia wziętych: Zobacz matematykę w otaczającym Cię świecie

Matematyka często wydaje się abstrakcyjna i oderwana od rzeczywistości. Nic bardziej mylnego! Jest ona wszędzie wokół nas, a odnoszenie problemów matematycznych do sytuacji z życia codziennego znacząco zwiększa zrozumienie i motywację do nauki. Kiedy widzisz praktyczne zastosowanie, nagle "po co mi to?" zamienia się w "aha, dlatego!".

Pomyśl o tym: procenty są w sklepach (rabaty, podwyżki), w bankach (kredyty, lokaty). Geometria jest w architekturze, projektowaniu wnętrz, nawet w grach komputerowych. Funkcje opisują ruch obiektów, wzrost populacji, zmiany kursów walut. Prawdopodobieństwo jest w prognozach pogody, loteriach, analizie ryzyka. Kiedy uczysz się o ułamkach, pomyśl o krojeniu pizzy. Kiedy o proporcjach, pomyśl o przepisach kulinarnych. Szukaj matematyki w swoich pasjach w sporcie, muzyce, sztuce, programowaniu. Zobaczysz, jak nagle abstrakcyjne pojęcia nabierają sensu i stają się dużo łatwiejsze do przyswojenia.

Narzędzia i zasoby, które wesprą Twoją naukę matematyki

W dzisiejszych czasach mamy dostęp do niesamowitej liczby narzędzi i zasobów, które mogą znacząco ułatwić naukę matematyki. Wykorzystaj je mądrze, a zobaczysz, jak szybko zrobisz postępy.

Najlepsze aplikacje mobilne do nauki matematyki Twój trener w kieszeni

Twój smartfon może być nie tylko źródłem rozrywki, ale i potężnym narzędziem do nauki. Istnieje wiele aplikacji mobilnych, które oferują interaktywne ćwiczenia, rozwiązania krok po kroku i natychmiastową informację zwrotną. Oto kilka, które polecam:

• Photomath: Wystarczy zeskanować zadanie aparatem telefonu, a aplikacja poda rozwiązanie krok po kroku. Idealna do sprawdzania swoich wyników i zrozumienia procesu.
• Microsoft Math Solver: Podobnie jak Photomath, rozwiązuje zadania, ale oferuje też wykresy, filmy instruktażowe i ćwiczenia.
• Khan Academy: Chociaż to platforma, ma też świetną aplikację mobilną. Oferuje tysiące lekcji wideo i interaktywnych ćwiczeń z matematyki na wszystkich poziomach.
• Geogebra: Niezastąpiona do wizualizacji funkcji, geometrii i algebry. Pozwala tworzyć dynamiczne konstrukcje i wykresy.
• Anki/Quizlet: Aplikacje do tworzenia fiszek i powtórek w systemie Spaced Repetition, idealne do zapamiętywania wzorów i definicji.

Platformy e-learningowe i kanały na YouTube, które warto znać (polskie i zagraniczne)

Internet to skarbnica wiedzy. Możesz uczyć się od najlepszych nauczycieli z całego świata, często zupełnie za darmo. Sam często korzystam z tych zasobów, aby odświeżyć swoją wiedzę lub znaleźć nowe sposoby na wyjaśnienie trudnych zagadnień.

• Khan Academy (PL/EN): Absolutny lider w edukacji online. Oferuje kompleksowe kursy z matematyki od podstawówki po studia, z lekcjami wideo, ćwiczeniami i testami. Dostępna w języku polskim.
• Matemaks.pl: Polska platforma z materiałami do matury i egzaminu ósmoklasisty. Mnóstwo zadań, teorii i rozwiązań.
• Pistacja.tv: Darmowe lekcje wideo z matematyki dla szkół podstawowych i średnich, tworzone przez polskich nauczycieli.
• Kanały na YouTube (polskie): "Matematyka Gryzie", "Matma z Pasją", "Matematyka w pigułce" oferują przystępne wyjaśnienia i rozwiązania zadań.
• Kanały na YouTube (zagraniczne): "3Blue1Brown" (dla wizualizacji i intuicyjnego zrozumienia), "Eddie Woo" (świetne wyjaśnienia), "Professor Leonard" (długie, szczegółowe wykłady).

Jak mądrze korzystać z kalkulatorów i programów matematycznych, by sobie pomagać, a nie szkodzić

Kalkulatory i programy matematyczne to potężne narzędzia, ale jak każde narzędzie, mogą być używane mądrze lub głupio. Moja zasada jest prosta: narzędzia te powinny wspierać Twoje zrozumienie, a nie zastępować myślenie.

Używaj kalkulatora do:

• Sprawdzania wyników swoich obliczeń.
• Wykonywania skomplikowanych rachunków, które nie są celem zadania (np. obliczanie wartości funkcji trygonometrycznych).
• Wizualizacji funkcji (np. kalkulatory graficzne).

Nie używaj kalkulatora do:

• Wykonywania podstawowych działań, które powinieneś umieć liczyć w pamięci (np. proste dodawanie, odejmowanie, mnożenie).
• Znajdowania gotowych rozwiązań bez próby samodzielnego zrozumienia problemu.

Pamiętaj, że na egzaminach często masz ograniczony dostęp do kalkulatora lub wcale go nie masz. Rozwijaj swoje umiejętności liczenia w pamięci i na kartce to podstawa. Kalkulator to pomocnik, nie zastępstwo dla Twojego mózgu.

Odblokuj swój potencjał: Utrzymaj motywację i czerp satysfakcję z nauki

Opanowanie matematyki to nie tylko kwestia technik, ale także psychologii. Utrzymanie motywacji i czerpanie satysfakcji z procesu nauki jest równie ważne, co znajomość wzorów. Chcę, abyś poczuł, że matematyka może być źródłem radości i dumy.

Ustawiaj małe, osiągalne cele: Metoda małych kroków w drodze na matematyczny szczyt

Wielkie cele, takie jak "zdać maturę z matematyki na 90%" mogą być przytłaczające. Dużo skuteczniejsza jest metoda małych kroków. Zamiast patrzeć na cały szczyt, skup się na zdobywaniu kolejnych, małych pagórków. Ustawiaj sobie małe, osiągalne cele, które możesz zrealizować w ciągu jednej sesji nauki lub jednego dnia. Na przykład: "Dziś rozwiążę 5 zadań z równań liniowych", "Dziś zrozumiem definicję pochodnej", "Dziś powtórzę wzory na pola figur płaskich".

Każde osiągnięcie takiego małego celu daje Ci poczucie sukcesu, buduje pewność siebie i napędza do dalszej pracy. Te małe sukcesy kumulują się, a zanim się obejrzysz, okaże się, że zdobyłeś znacznie większy "szczyt", niż początkowo myślałeś. To jak budowanie muru nie budujesz go od razu, ale układasz cegłę po cegle.

Znajdź swoje "dlaczego": Jak odkryć praktyczne zastosowania matematyki w Twoich pasjach

Motywacja wewnętrzna jest najsilniejszą siłą napędową. Zamiast uczyć się matematyki, bo "musisz", spróbuj znaleźć swoje osobiste "dlaczego". Jak matematyka łączy się z Twoimi pasjami i zainteresowaniami? Jeśli kochasz gry komputerowe, zrozum, że matematyka jest podstawą ich programowania i grafiki. Jeśli interesujesz się muzyką, odkryj matematyczne proporcje w harmonii i rytmie. Jeśli marzysz o karierze w medycynie, zrozum, jak matematyka pomaga w analizie danych medycznych i modelowaniu chorób. Jeśli interesuje Cię ekonomia, zobacz, jak matematyka jest narzędziem do przewidywania rynków i zarządzania finansami. Kiedy połączysz matematykę z czymś, co naprawdę Cię pociąga, nauka przestanie być obowiązkiem, a stanie się fascynującą podróżą.

Nauka w grupie czy samodzielnie? Odkryj, co jest dla Ciebie lepsze i jak to wykorzystać

Nie ma jednej uniwersalnej metody nauki, która pasowałaby każdemu. Niektórzy kwitną w grupie, inni potrzebują spokoju i samotności. Ważne jest, abyś odkrył, co działa najlepiej dla Ciebie i jak to wykorzystać.

Nauka w grupie:

• Zalety: Możliwość wzajemnego tłumaczenia sobie zagadnień (Technika Feynmana!), wspólne rozwiązywanie trudnych zadań, motywacja wzajemna, natychmiastowa informacja zwrotna, różnorodność perspektyw.
• Wady: Ryzyko rozpraszania się, dominacja jednej osoby, nierówny poziom wiedzy.

• Zalety: Pełna koncentracja, możliwość dostosowania tempa i metod do własnych potrzeb, budowanie samodzielności w rozwiązywaniu problemów.
• Wady: Brak natychmiastowej pomocy w razie trudności, ryzyko utknięcia w martwym punkcie, brak perspektywy z zewnątrz.

Moja rada: spróbuj obu metod. Może okazać się, że najlepiej działa dla Ciebie połączenie samodzielna nauka teorii i rozwiązywanie prostszych zadań, a następnie spotkania w grupie w celu omówienia trudniejszych problemów i wzajemnego testowania się.

Przeczytaj również: Jak uczy się mózg? Odkryj sekrety efektywnej nauki i pamięci

Kiedy warto sięgnąć po pomoc? Rola korepetytora w procesie nauki

Często widzę, jak uczniowie zmagają się w samotności, bojąc się prosić o pomoc. To błąd! Czasem, pomimo najlepszych chęci i stosowania wszystkich technik, po prostu potrzebujemy wsparcia z zewnątrz. Rola korepetytora w procesie nauki jest nieoceniona, zwłaszcza gdy masz duże braki lub zmagasz się z konkretnym zagadnieniem.

Korepetytor może:

• Zdiagnozować Twoje braki i pomóc Ci je uzupełnić w spersonalizowany sposób.
• Wyjaśnić trudne zagadnienia w sposób, który jest dla Ciebie zrozumiały.
• Dostarczyć dodatkowe materiały i zadania dostosowane do Twojego poziomu.
• Zmotywować Cię i zbudować Twoją pewność siebie.
• Nauczyć Cię efektywnych strategii rozwiązywania problemów.

Nie traktuj korepetycji jako oznaki słabości, ale jako mądrą inwestycję w swoją edukację. To jeden z najczęściej poszukiwanych obszarów wsparcia w nauce, co świadczy o jego skuteczności. Czasem jedna godzina z dobrym korepetytorem może wyjaśnić więcej niż tygodnie samodzielnych zmagań.